生成式对抗网络（GAN）学习笔记

对于潜在的公式渲染错误，新的处置方案包括已正确渲染的 PDF 文件和已正确渲染的 HTML。
04/12/2023 KevinZonda

GAN 是一个的网络，其将一个无监督学习问题巧妙转换成了监督学习问题。其核心包含了两组神经网络：生成器（$G$）和辨别器（$D$）。

生成器的目的是通过输入 $z$，生成假数据 $G(z)$。

辨别器的目的是根据输入，输出输入是真实的置信度。也就是判定是真实数据还是假数据：如果是真实数据，输出 1；如果是假数据，输出 0。

因此我们的目标可以简化为，我们希望构建一个足够好的辨别器，并让生成器成功欺骗辨别器。

建模

生成器 $G$

对于生成器 $G$，其输入是一个随机噪声 $z\sim p_{z}(z)$，输出是一个假数据 $G(z)$。

其目标是使得辨别器 $D$ 无法判定 $G(z)$ 是假数据。因此则为： $$ \max D(G(z)) $$

辨别器 $D$

对于辨别器 $D$，其输入是一个数据，输出 $D(x)$ 是一个概率，表示 $x$ 是真实数据的概率。

因此对于真实数据： $x\sim p_{data}(x)$，我们期望

$$ \max D(x) $$

因此对于虚假数据（生成的数据）： $z\sim p_{z}(z)$，我们期望

$$ \min D(G(z)) $$

目标函数

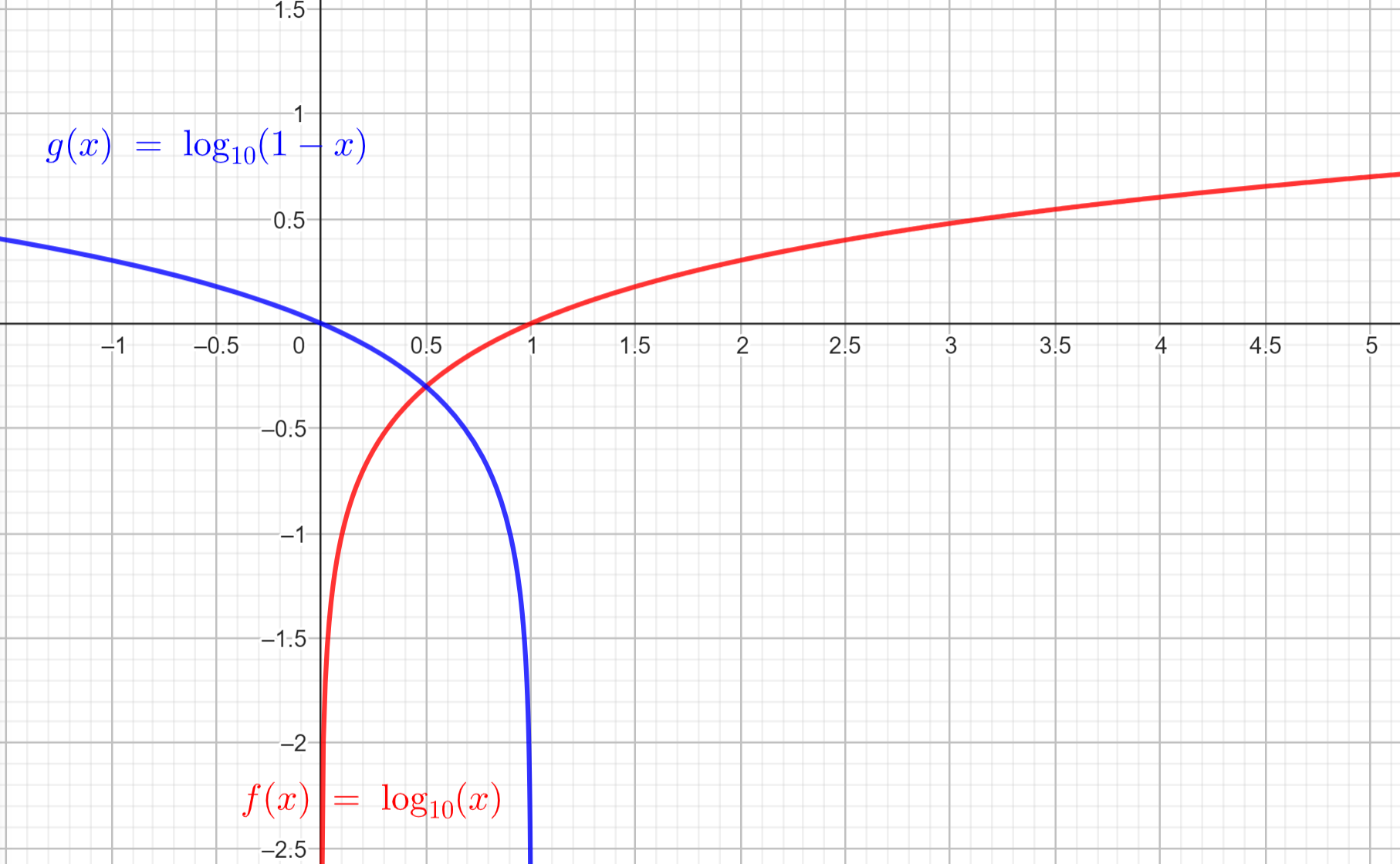
为此可以构建目标函数：

$$ \min_{G}\max_{D} V(D, G) = \mathbb{E}_{x\sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_{data}(z)}[\log(1-D(G(z)))] $$

对于辨别器 $D$：

期望 $D(x)$ 大
期望 $D(G(z))$ 小
- $\rightarrow 1-D(G(z))$ 大
- $\rightarrow \log{(1-D(G(z)))}$ 大
因此期望 $V(D, G)$ 大

对于生成器 $G$：

期望 $D(G(z))$ 大
- $\rightarrow 1-D(G(z))$ 小
- $\rightarrow \log{(1-D(G(z)))}$ 小
因此期望 $V(D, G)$ 小

我们可以理解数学期望 $\mathbb{E}$ 为:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
func E(xs []float64,
      oper func(float64) float64
     ) float64 {
   sum := 0.0
   count := 0
   for _, x := range xs {
       sum += oper(x)
       count++
   }
   sum /= count
   return sum
}

算法 1

对于 每一个迭代 循环：
- 循环 k 次（需要自定义）
  - 从噪音分布 $p_g(z)$ 中采样 $m$ 个噪音样本 ${z^{(1)}, \dots, z^{(m)}}$
  - 从真实数据分布 $p_{data}(x)$ 中采样 $m$ 个真实样本 ${x^{(1)}, \dots, x^{(m)}}$
  - 更新辨别器 $D$ 的参数：
    - $\theta_{D} \leftarrow \theta_{D} - \alpha \nabla_{\theta_{D}} \frac{1}{m} \sum_{i=1}^{m} \left[ \log D(x^{(i)}) + \log (1-D(G(z^{(i)}))) \right]$
  - 结束循环
- 从噪音分布 $p_g(z)$ 中采样 $m$ 个噪音样本 ${z^{(1)}, \dots, z^{(m)}}$
- 更新生成器 $G$ 的参数：
  - $\theta_{G} \leftarrow \theta_{g} - \alpha \nabla_{\theta_{G}} \frac{1}{m} \sum_{i=1}^{m} \log (1-D(G(z^{(i)})))$
结束循环

需要注意，在最开始时候 $D$ 可能训练的特别好，但是 $G$ 很难训练的很好，那么 $G$ 就会面对梯度消失的问题。

可能的解决方案，使用最大化 $\log D(G(z))$，而不是最小化 $\log (1-D(G(z)))$ 以训练 $G$。

理论证明

命题 1：最佳的 $D$

Proposition 1：对于固定的 $G$，最佳的 $D$ 是

$$ D^{*}_{G}(x) = \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)}\in[0, 1] $$

对于两个分布 $p_{data}$ 和 $p_g$，为了判别其是否相等，原式=.5（Two Sample Test）。

证明：

考虑：

$$ \mathbb{E}_{x\sim p} f(x) = \int_{x} p(x)f(x)dx $$

可得：

$$ \begin{align} V(D, G) &= \mathbb{E}_{x\sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_{data}(z)}[\log(1-D(G(z)))] \\ &= \int_{x} p_{data}(x)\log D(x)dx + \int_{z} p_{z}(z)\log(1-D(G(z)))dz \\ &\text{考虑 } G(z)=p_g(x) \\ &= \int_{x} p_{data}(x)\log D(x)dx + \int_{x} p_{g}(x)\log(1-D(x))dx \\ &= \int_{x} p_{data}(x)\log D(x) + p_{g}(x)\log(1-D(x))dx \end{align} $$

令

$$ \begin{align} a &= p_{data}(x) \\ y &= D(x) \\ b &=p_{g}(x) \end{align} $$

因此可使原式改写为

$$ \begin{align} V(D, G) &= \int_{x} p_{data}(x)\log D(x) + p_{g}(x)\log(1-D(x))dx \\ &=\int_{x}a\log (y)+b\log(1-y)dx \end{align} $$

考虑到这是一个关于辨别器的函数，也就是对于 $D$的函数，因此我们认为这个函数是 $y\to a\log(y)+b\log(1-y)$

这个函数是个凸函数，因此为求其最大值，我们可以求其导数为0的点。

$$ \begin{align} \frac{d}{dy}a\log(y)+b\log(1-y) &= \frac{a}{y} - \frac{b}{1-y} = 0 \\ \frac{a}{y} &= \frac{b}{1-y} \\ a - ay &= by \\ y &= \frac{a}{a+b} \\ D(x) &= \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)} \end{align} $$

代入回原式，可得：

$$ \begin{align} C(G) &= \max_{D}V(D, G) \\ &= \mathbb{E}_{x \sim p_{data}(x)}[\log (D^{*}_{G}(x))] + \mathbb{E}_{z \sim p_{z}(z)} [\log (1-D^{*}_{G}(G(z)))] \\ &= \mathbb{E}_{x \sim p_{data}}[\log (D^{*}_{G}(x))] + \mathbb{E}_{x \sim p_{g}} [\log (1-D^{*}_{G}(x))] \\ &= \mathbb{E}_{x \sim p_{data}}\left[ \log \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)} \right] + \mathbb{E}_{x \sim p_{g}} \left[\log \frac{p_{g}(x)}{p_{data}(x) + p_{g}(x)}\right] \end{align} $$

因为我们已经完成了最大化 D，因此只需要最小化 $C(G)$ 了。

KL 散度
$$ D_{KL}(P||Q) = \mathbb{E}_{x\sim p(x)}\log \frac{P(x)}{Q(x)}\ = \sum_i P(i) \log \frac{P(i)}{Q(i)} $$
有两个分布 $P$ 和 $Q$，我们希望知道 $P$ 和 $Q$ 之间的差异。

定理 1：$C(G)$ 的最小值

定理 1：当且仅当 $p_g = p_{data}$ 时，$C(G)$ 达到全局最小解。并且此时 $C(G) = - \log 4$

证明：

考虑当 $D$ 达到 optimal 时候，$D(x)=\frac{1}{2}$。因此 $$ C(G)=\log \frac{1}{2} + \log \frac{1}{2} = - \log 4 $$

因此可以重写原式：

$$ \begin{align} C(G) &= \mathbb{E}_{x \sim p_{data}}\left[ \log \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)} \right] + \mathbb{E}_{x \sim p_{g}} \left[\log \frac{p_{g}(x)}{p_{data}(x) + p_{g}(x)}\right] \\ &= \left( \mathbb{E}_{x \sim p_{data}}\left[ \log \frac{p_{data}(x)}{\frac{1}{2}(p_{data}(x) + p_{g}(x))} \right] - \log 2 \right) + \left( \mathbb{E}_{x \sim p_{g}} \left[\log \frac{p_{g}(x)}{\frac{1}{2}(p_{data}(x) + p_{g}(x))}\right] - \log 2 \right) \\ &= - \log 4 + D_{KL}\left(p_{data}||\frac{p_{data}+p_{g}}{2}\right)+ D_{KL}\left(p_{g}||\frac{p_{data}+p_{g}}{2}\right) \end{align} $$

考虑 KL 散度的性质：KL散度 $\geq 0$，当其为 0 时，必然是两分布相同，因此为让 $C(G)$ 最小，我们需要让 KL 散度最小，也就是 $p_{data} = p_{g}$。

算法 1 的收敛性

命题 2

proposition 2：如果 $G$ 和 $D$ 有足够的容量（capacity），并且对于算法 1的每一步，辨别器 $D$ 和 $p_g$ 在给定 $G$ 被训练到最优，使用如下标准：

$$ \mathbb{E}_{x \sim p_{data}}\left[ \log D^*_G(x) \right] + \mathbb{E}_{x \sim p_{g} }\left[ \log (1 - D^*_G(x)) \right] $$

那么 $p_g$ 收敛到 $p_{data}$。

Contents

建模